Previously in the posts, Representing The Circle and Polygonal Convergence, the relationship between circles, polygons and convergences was discussed. Delving deeper into the possibilities that materialise out of these associations yields Convergent Polygon Spirals. These types of Spirals are generated by tracking a point on each subsequent propagation of a particular Polygonal Convergence pattern and fitting a smooth curve through them.

For example, the way a Quadragon Spiral is created appears in the diagram above. The Connecting Points image uses straight line segments to show the polygon vertices that are to be connected via the emergent Spiral. The Smooth Spiral image is what arises when a spline curve is fitted to those points.
These connecting points are determined by,
- Selecting a vertex on the outer most polygon of a convergence pattern.
- Rotate either clockwise or anti-clockwise around the centre of the circle/polygon, while also transitioning inward to the next polygon in the convergence.
- Upon rotating an amount that is equivalent to the Polygonal Angle, the next point is located at the vertex of this subsequent polygon.
- Repeat steps 2 and 3 for however many vertices are to be connected in the developing Polygon Spiral.
Spiral Density
Polygonal Convergences with higher order regular polygons produce denser convergence patterns. It follows then, that Spirals generated from these higher order Polygonal Convergences will produce denser Spirals, as is shown to be the case in the Polygon Spiral Density diagram below.
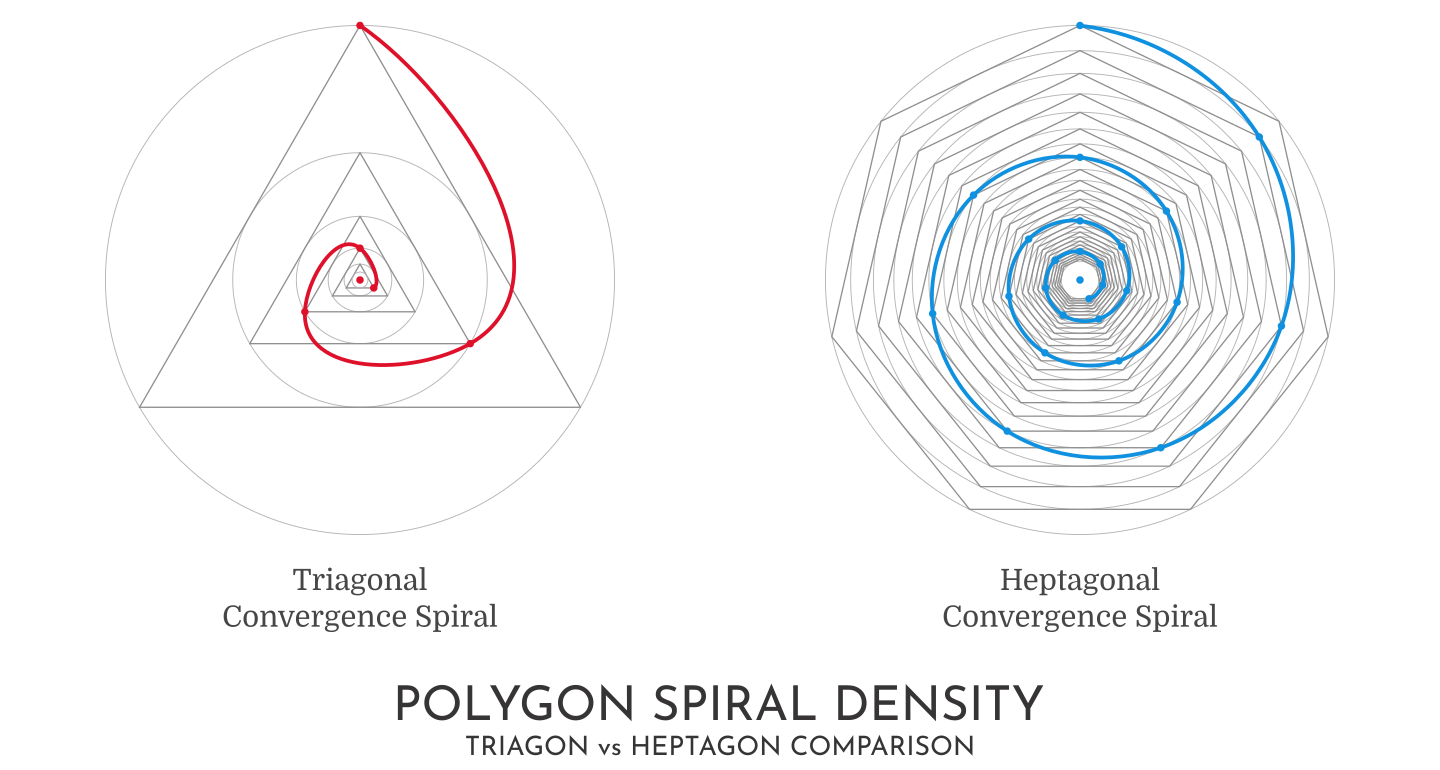
However, when examining a Heptagonal Convergence Spiral, not only does it display more revolutions than a Triagonal Convergence Spiral, the resultant curve of the Heptagonal Spiral exhibit’s gentler transitions through all its connecting vertices.
The Triagonal Spiral possesses a characteristic lobe prior to its transitions. The reason for this is a combination of a greater disparity between the parent Triagon and its convergent offshoot, plus a larger Polygonal Angle it must rotate through while bridging one vertex point to the next. Thus requiring a more abrupt change in direction as a way to keep the consequent curve smooth.
Spiral Convergence Comparison
Polygonal Convergences have two fundamental variances, Symmetric Convergence and Asymmetric Convergence and Spirals can be generated from either variant.
Previous examples above have been founded on Symmetric Convergences, but the diagram below shows the different outcomes obtained by both Symmetric and Asymmetric Convergence, using the Hexagon as a base.

What this comparison reveals, is that the Asymmetric Convergence Spiral exhibits fewer revolutions compared to its Symmetric counterpart, in a way similar to the Spiral generated with a Triagon source. But it does not possess the characteristic lobe of the Triagonal Convergence Spiral, instead offering a more gradual transition through the vertices of each polygon.
Polygon Spiral Arms
Finally, not only do these Polygonal Convergence patterns generate one Spiral, but can produce a Spiral for each vertex of the particular foundational polygon. For example, with the Pentagon having five vertices, it provides the framework for up to five separate Pentagonal Convergence Spirals.
In closing, Polygonal Convergences and Spirals not only furnish interesting forms in their own right, but can also be used more discretely, by providing the proportional metric for defining scale and elemental relationships within a geometric or artistic composition. Essentially, they can be used as the supportive framework for many types of design work, with their versatility being limited only by imagination.


