Regular polygons present natural convergences and divergences when coupled with their circumscribed and inscribed circles. This post will primarily deal with the convergence aspect, as divergence follows a similar template, only in the opposite direction.
Polygonal Convergence is the term that will be used to describe the diminishing pattern that is created when the inscribed circle of a regular polygon becomes the circumscribed circle for the next iteration of the parent polygon.
The larger Quadragon in the above diagram is shown with its circumscribed and inscribed circles.
In the Polygonal Convergence process the inscribed circle becomes the circumscribed circle for the next polygon in the sequence and following from that, the next inscribed circle is generated.
A convergence pattern follows a structured reduction progression and each subsequent polygon will be reduced by the same factor from its predecessor. This Polygonal Convergence Factor is unique to each specific regular polygon and can be readily ascertained by following the steps below.
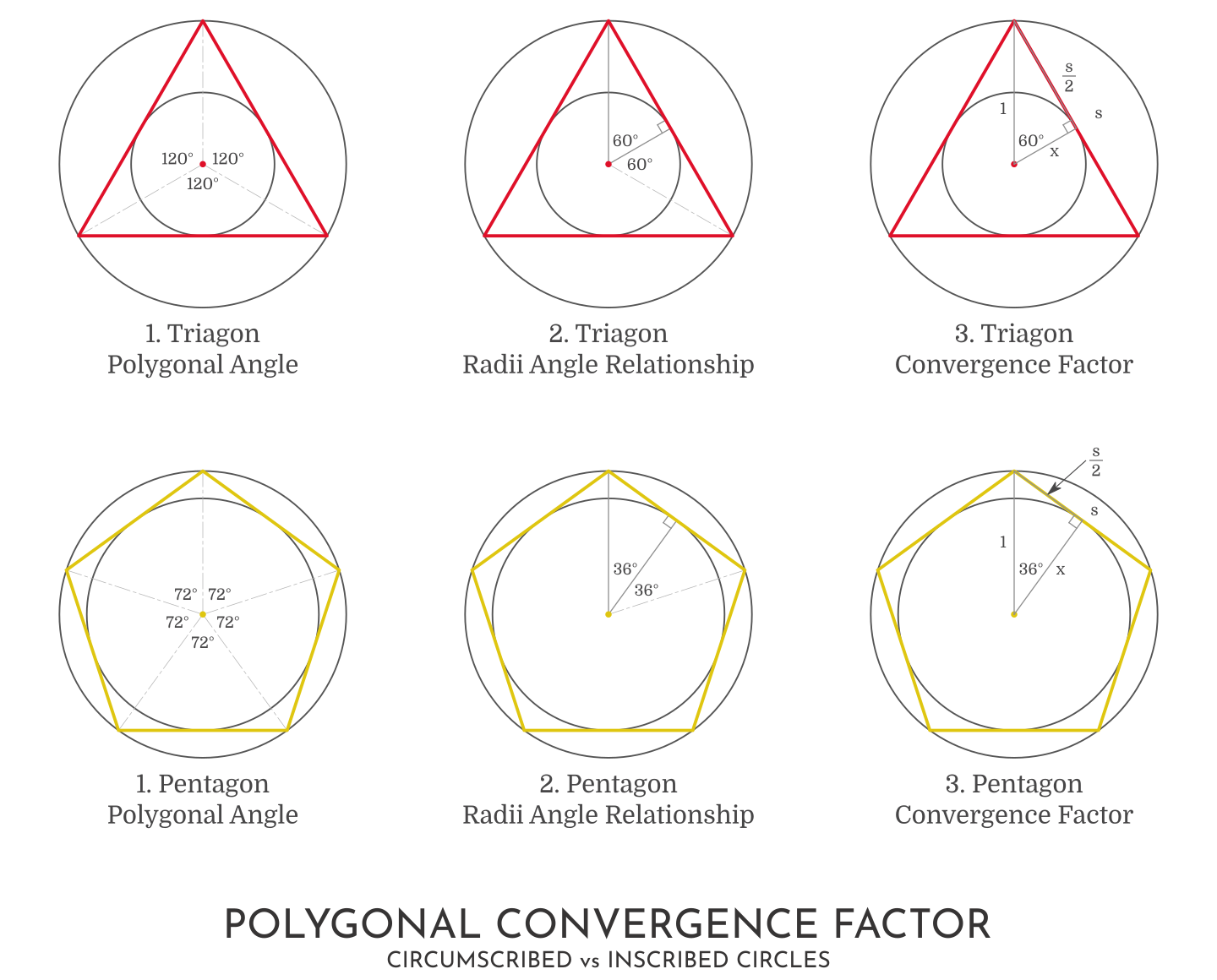
1. Polygonal Angle
The first item that is to be determined is the Polygonal Angle and this angle is produced by extending two connecting lines from the centre of the polygon to two adjacent vertices.
In the case of the Triagon, the Polygonal Angle is 120° and for the Pentagon it is 72°, as shown in the above diagram.
To determine this angle, simply divide 360° by the number of vertices found on the regular polygon in question.
The reason for this, is that the vertices in a regular polygon are dividing the circle equally. Therefore, the angle formed by two connecting lines from the centre, to two adjacent vertices, will be the Polygonal Angle.
Polygonal\space Angle=\frac{360°}{n}Where,
360° = One revolution of a circle.
n = Number of regular polygon vertices.
The number of vertices happens to also correspond with the number of polygon line segments.
2. Radii Angle Relationship
Next, by extending a line from the centre of the circle/polygon to the intersection point of the inscribed circle and polygon, creates a right-angle triangle. This intersection point coincides with the midpoint of the polygon line segment, since the inscribed circle is tangential to this line segment at its midpoint.
Establishing this right-angle triangle now defines a relationship between the radius of the circumscribed circle and the radius of the inscribed circle, with the angle between the two being half the Polygonal Angle.
3. Convergence Factor
Finally, by using trigonometric relationships, the length of the inscribed circle radius can be resolved. In the case of the Triagon, the trigonometric relationship which determines the inscribed circle radius, x, is,
\cos(60°)=\frac{x}{1}\\
\space\\
x = \cos(60°)\\
\space\\
x = 0.5Where,
60° = Half the Polygonal Angle of a Triagon.
x = Inscribed circle radius.
1 = Circumscribed circle radius.
So what this now gives is the Polygonal Convergence Factor for the Triagon, because the original circumscribed circle radius is set to 1.
This means that each subsequent Triagon in a Triagonal Convergence will be reduced in size by a factor of 0.5 from its predecessor.
A generalised representation of this relationship which is applicable to all regular polygons is,
x = \cos(\frac{360°}{2n})\\
\space\\
x = \cos(\frac{180°}{n})Where,
x = Polygonal Convergence Factor.
n = Number of regular polygon vertices.
360°/2, takes into account that half the Polygonal Angle defines this relationship.
The table below shows the Polygonal Angle and Convergence Factors for the first nine regular polygons.
| POLYGON | NUMBER OF VERTICES | POLYGONAL ANGLE | CONVERGENCE FACTOR EQUATION | POLYGONAL CONVERGENCE FACTOR |
|---|---|---|---|---|
| Triagon | 3 | 120° | cos(60°) | 0.5 |
| Quadragon | 4 | 90° | cos(45°) | 0.7071 |
| Pentagon | 5 | 72° | cos(36°) | 0.8090 |
| Hexagon | 6 | 60° | cos(30°) | 0.8660 |
| Heptagon | 7 | 51.43° | cos(25.71°) | 0.9010 |
| Octagon | 8 | 45° | cos(22.5°) | 0.9239 |
| Nonagon | 9 | 40° | cos(20°) | 0.9397 |
| Decagon | 10 | 36° | cos(18°) | 0.9511 |
| Hendecagon | 11 | 32.73° | cos(16.36°) | 0.9595 |
| TABLE 1 |
Some of these Convergence Factors present interesting proportions.
Triagon = \frac{1}{2}\\
\space\\
Quadragon = \frac{\sqrt{2}}{2}\\
\space\\
Pentagon = \frac{\phi}{2}\\
\space\\
Hexagon = \frac{\sqrt{3}}{2}\\
\space\\
\space\\
Where\space \phi\space (phi)\space is\space the\space Golden\space Ratio
\space\\
\space\\
\space\\
Convergence Density
As has been established in Table 1, these Polygonal Convergence Factors approach 1 as the number of vertices is increased. This then leads to convergence patterns that increase in density with the higher order polygons.
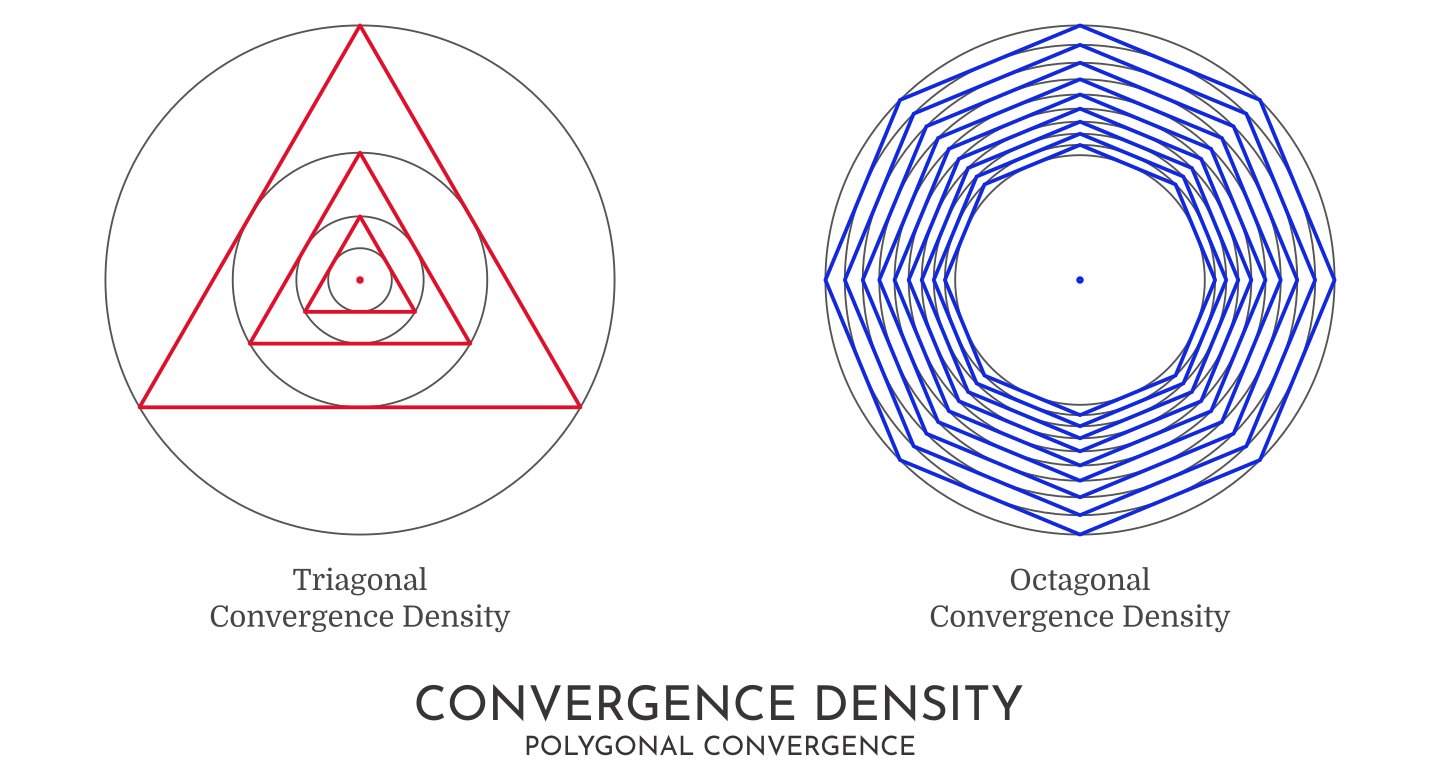
Symmetric Convergence
Symmetric Convergence is a term that defines convergence patterns where the subsequent convergent polygon has the same angular orientation as its predecessor.
Asymmetric Convergence
The term Asymmetric Convergence is used to define convergence patterns where the successive convergent polygon is rotated by half its Polygonal Angle as compared to its predecessor.
These types of geometric patterns and structures could be considered Inwardly Infinitely Self-Reflecting, since the convergent figure is a fractal image of its predecessor and the process can be continued indefinitely.




